Tree-structured Attention with Hierarchical Accumulation

Abstract

Incorporating hierarchical structures like constituency trees has been shown to be effective for various natural language processing (NLP) tasks. However, it is evident that state-of-the-art (SOTA) sequence-based models like the Transformer struggle to encode such structures inherently. On the other hand, dedicated models like the Tree-LSTM, while explicitly modeling hierarchical structures, do not perform as efficiently as the Transformer. In this paper, we attempt to bridge this gap with "Hierarchical Accumulation" to encode parse tree structures into self-attention at constant time complexity. Our approach outperforms SOTA methods in four IWSLT translation tasks and the WMT'14 English-German translation task. It also yields improvements over Transformer and Tree-LSTM on three text classification tasks. We further demonstrate that using hierarchical priors can compensate for data shortage, and that our model prefers phrase-level attentions over token-level attentions.

Summary

The underlying construction process of natural language is hierarchical, which reflects as grammars. NLP scientists model this characteristic by using Constituency tree, dependency tree, etc. However, state-of-the-art neural language models,like the Transformer, prefer to process the linear (sequential) form of language because it allows easier and efficient computations. For instance, the Transformer performs language processing at O(1) parallel time complexity.

On the other hand, dedicated models to process tree-like structures (e.g., Tree-LSTM) are recurrent or recursive, thus inefficient and non-scalable.

Our proposed method - Hierarchical Accumulation, meanwhile, operates at the same time complexity as the Transformer. It aggregates information in almost the same bottom-up manner as Tree-LSTM. Our experimental analyses show that the model assigns more attentions to phrases (or sub-trees) than individual words. The method is also shown to compensate for data shortage in certain low-resource setup.

Tree-Structure Hierarchical Accumulation

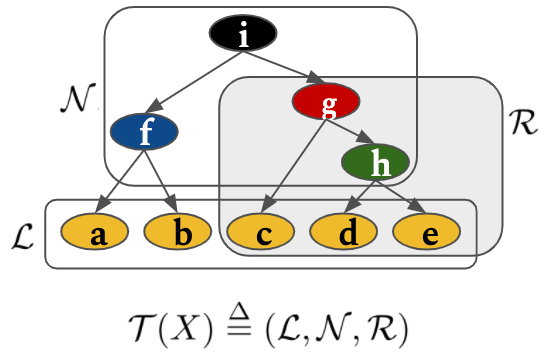
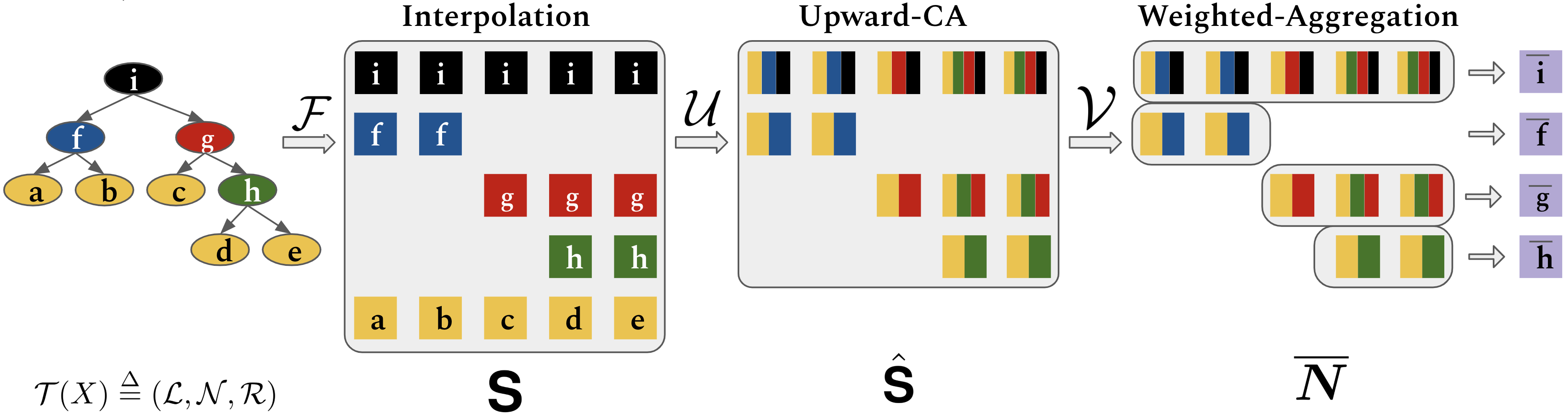
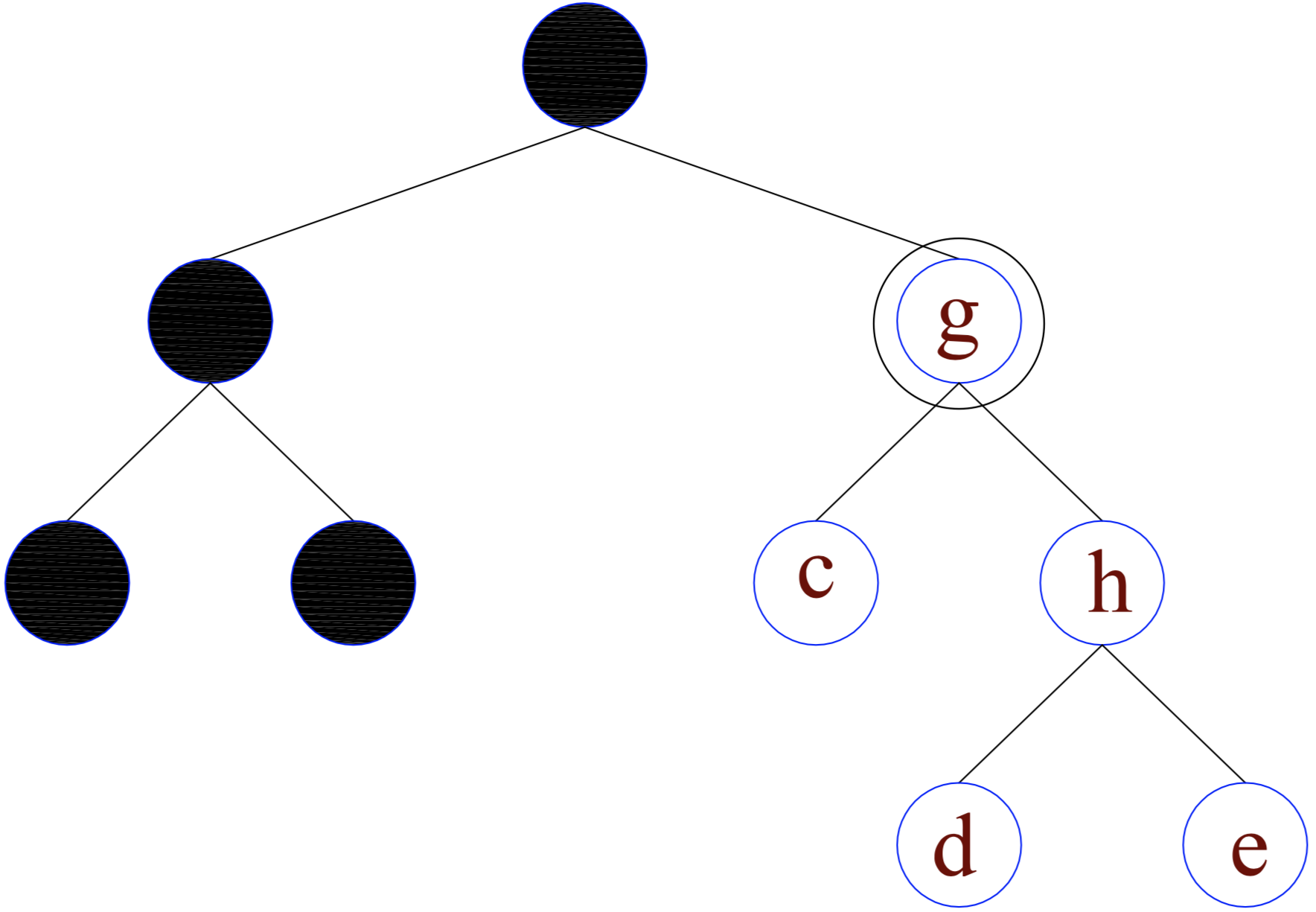
First, let's start with how we formulate trees in this method. We group the tree components nonterminal nodes, terminal nodes (leaves) as $\mathcal{N}$ and $\mathcal{L}$. Let $\mathcal{R}(x)$ denotes the set of all nodes that belong to the subtree rooted at $x$. For example, in the figure, $\mathcal{R}(g) = \{g, c, h, d, e\}$.

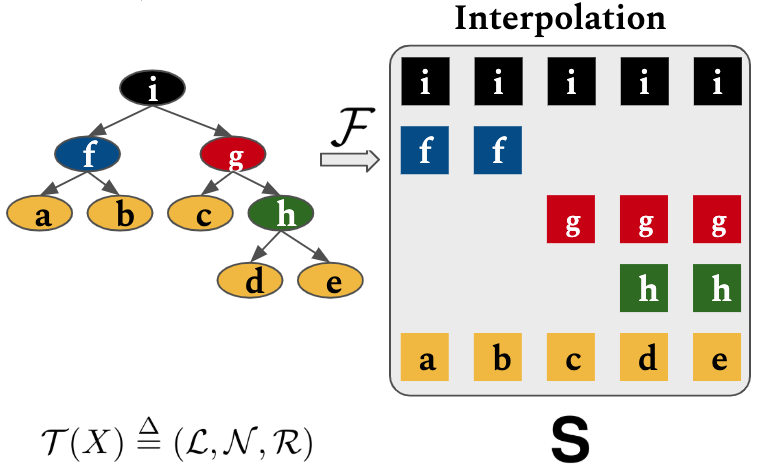
Then, let $\mathbf{L} \in \mathbb{R}^{n\times d}$ and $\mathbf{N} \in \mathbb{R}^{m\times d}$ be leaves and nonterminals. We define interpolation operation $\mathcal{F}: (\mathbb{R}^{n\times d}, \mathbb{R}^{m\times d}) \rightarrow \mathbb{R}^{(m+1)\times n \times d}$: \begin{equation} \mathbf{S}_{i,j} = \mathcal{F}(\mathbf{L},\mathbf{N},\mathcal{R})_{i,j} = \left\{ \begin{array}{ll} \mathbf{L}_{j} & \mbox{if } i = 1 \\ \mathbf{N}_{i-1} & \mbox{else if } x^{\mathcal{L}}_j \in \mathcal{R}(x^{\mathcal{N}}_{i-1}) \\ \mathbf{0} & \mbox{otherwise. } \end{array} \right. \end{equation}

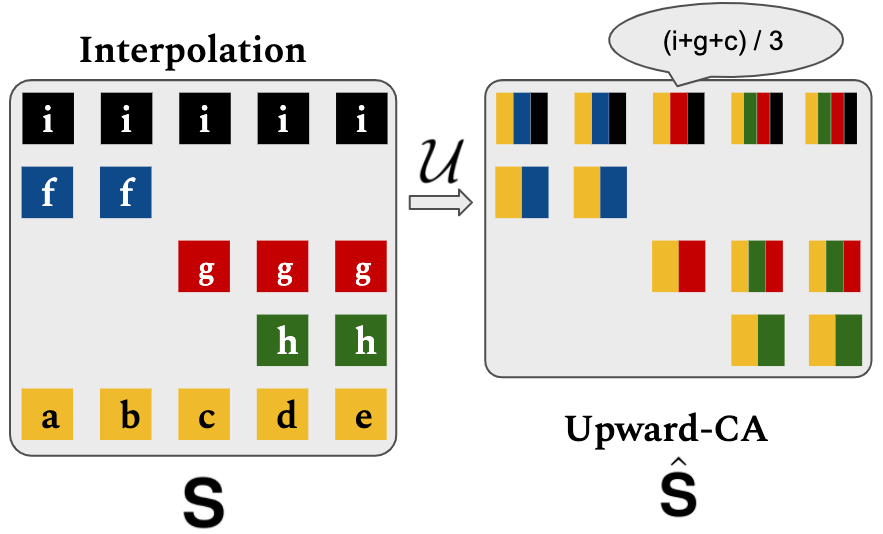
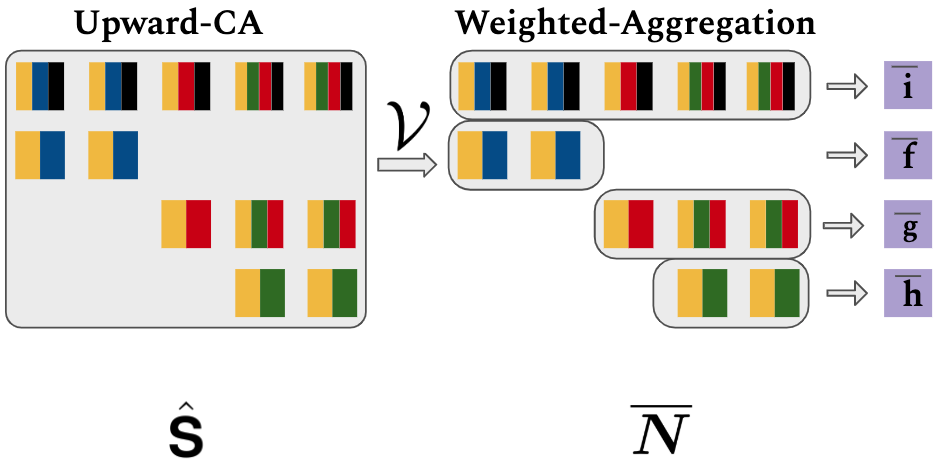
The next operation is Bottom-up Upward Cumulative Average $\mathcal{U}$. $\mathcal{U}$ composes node states in bottom-up fashion. \begin{equation} \mathcal{U}(\mathbf{S})_{i,j} = \hat{\mathbf{S}}_{i,j} = \left\{ \begin{array}{ll} \mathbf{0} & \mbox{if } \mathbf{S}_{i+1,j} = \mathbf{0}\\ \sum_{\mathbf{S}_{t,j} \in C_j^i} \mathbf{S}_{t,j} / {|C_j^i|} & \mbox{otherwise.} \\ \end{array} \right. \end{equation} where $C_j^i=\{\mathbf{S}_{1,j}\}\cup\{\mathbf{S}_{t,j}|x^{\mathcal{N}}_t \in \mathcal{R}(x^{\mathcal{N}}_i)\}$ is set nodes in branch $(x_i^{\mathcal{N}}\rightarrow x_j^{\mathcal{L}})$.

After that, Weighted Aggregation $\mathcal{V}$ combines branch-level representations of a node, resulting matrix $\overline{\mathbf{N}}=(\overline{\mathbf{n}}_1,...,\overline{\mathbf{n}}_m) \in \mathbb{R}^{m\times d}$. \begin{equation} \mathcal{V}(\hat{\mathbf{S}}, \mathbf{w})_{i} = \overline{\mathbf{n}}_{i} = \frac{1}{|\mathcal{L} \cap \mathcal{R}(x^{\mathcal{N}}_i)|}\sum_{j:x^{\mathcal{L}}_j \in \mathcal{R}(x^{\mathcal{N}}_i)} w_{j} \odot \hat{\mathbf{S}}_{i,j} \end{equation}

Overall, the hierarchical accumulation process can be summarized as follow:

Hierarchical Embeddings

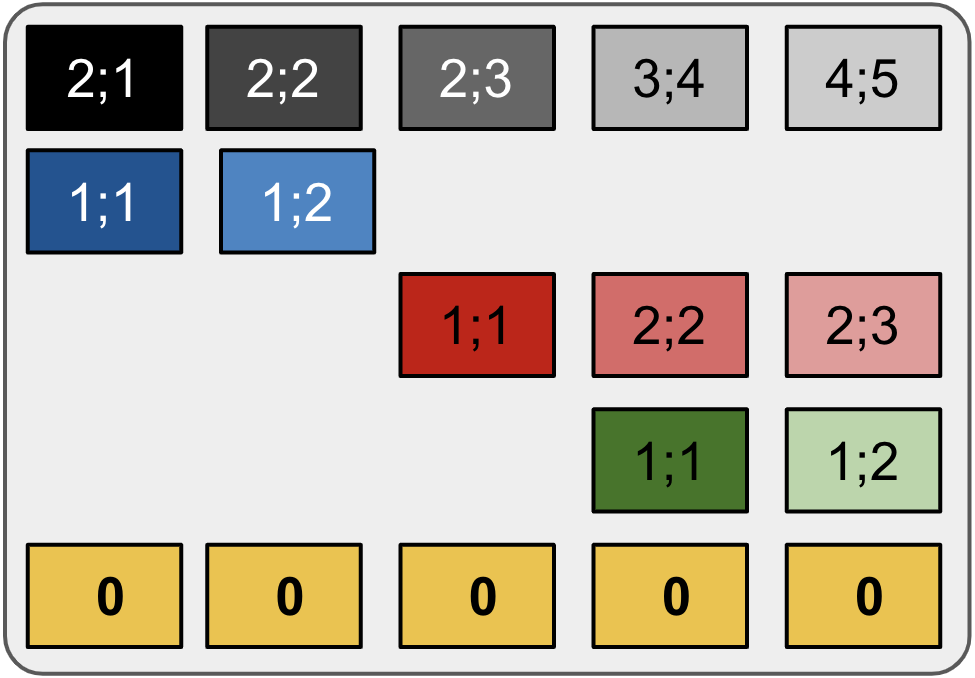
At this stage, each node treats its descendants equally. Though global tree structure is captured, local descendent relationships not differentiated. Thus we model such local relationships with hierarchical embeddings $\mathbf{E} \in \mathbb{R}^{(m+1)\times n \times d}$ \begin{equation} \mathbf{E}_{i,j} = \left\{ \begin{array}{ll} [\mathbf{e}^v_{|V_j^i|};\mathbf{e}^h_{|H_j^i|}] & \mbox{if } i > 1 \mbox{ and } x^{\mathcal{L}}_j \in \mathcal{R}(x^{\mathcal{N}}_i)\\ \mathbf{0} & \mbox{otherwise. }\\ \end{array} \right. \end{equation} where $V_j^i$ is $x_j^{\mathcal{L}}$'s ancestors up to $x_i^{\mathcal{N}}$, $H_j^i$ is set of leaves from leftmost leaf up to $x_j^{\mathcal{L}}$ of the $x_i^{\mathcal{N}}$-rooted subtree.
In the figure, each block $\mathbf{E}_{i,j}$ is an embedding vector $[\mathbf{e}^v_x;\mathbf{e}^h_y]$ with indices $x,y$ following syntax ``$x;y$'' in the block, where $x=|V_j^i|$ and $y=|H_j^i|$. ``$\mathbf{0}'' indicates no embedding.

Subtree masking

When computing attention, we also out the attention scores corresponding to nodes that do not belong to the target node's subtree, thus improving localization of attention.

Encoder Self-Attention and Decoder Cross-Attention

We apply our hierarchical accumulation method to the encoder self-attention and decoder cross-attention in the Transformer NMT framework. The figures below show how we design to incorporate the tree accumulation process in the layers. In particular, we maintain two components leaves and nonterminals for source tree while the target is kept as a sequence. In the figure, circle-ended arrows indicate wherehierarchical accumulations take place.

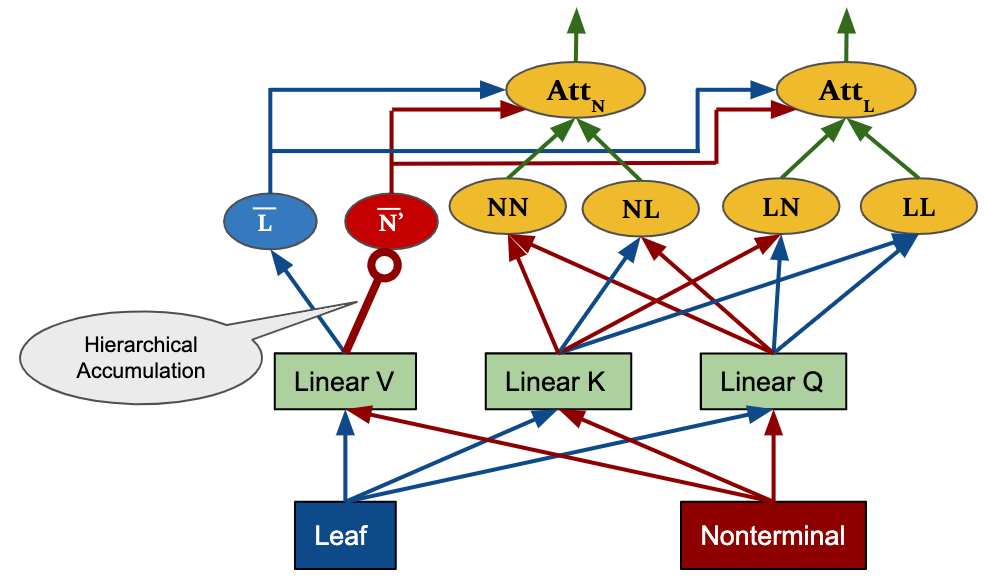
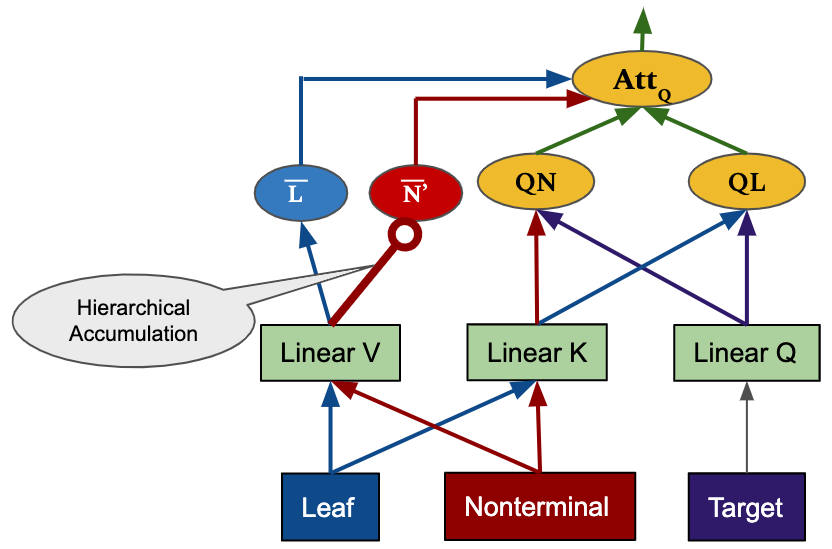
The overal Tree-structured Transformer network is designed as follow

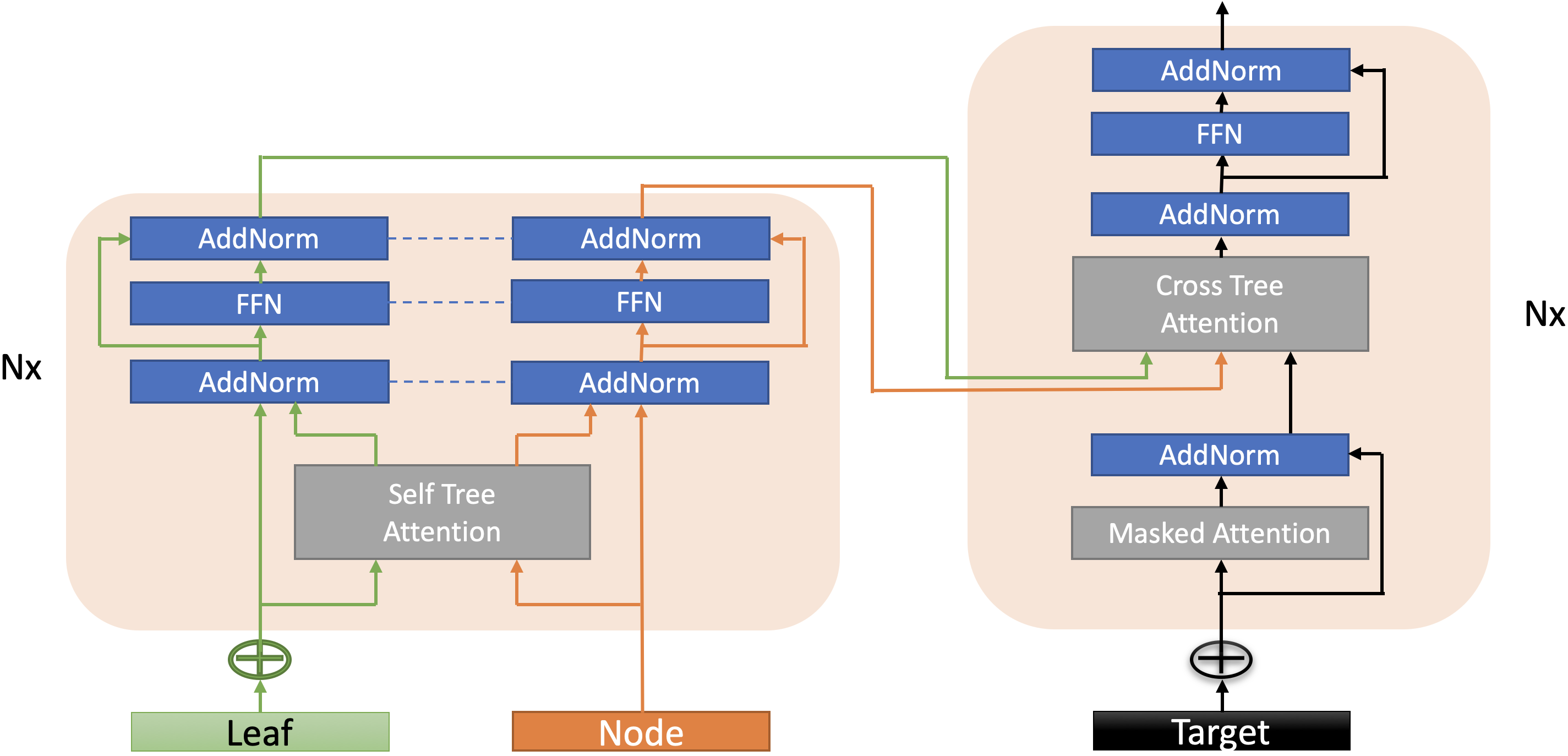
Experiments

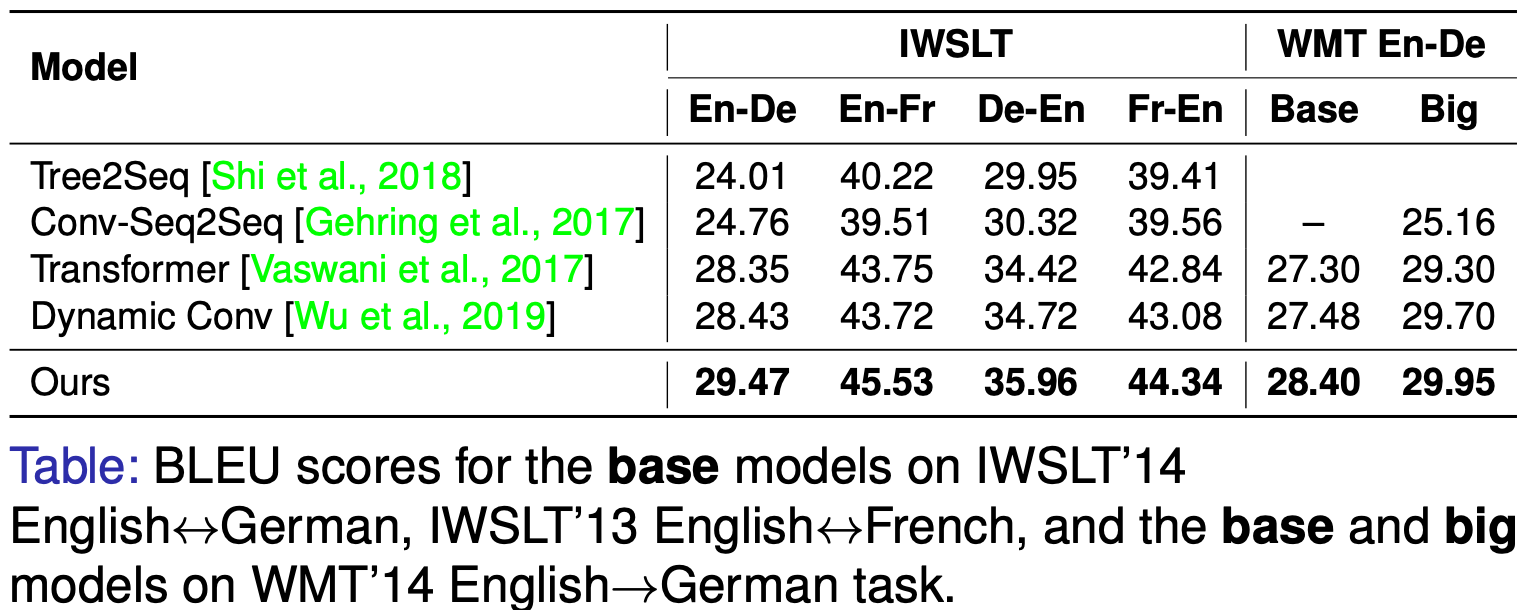
We conducted experiments on a variety of machine translation and text classification tasks. The following table shows the performance comparison of our method against other common baselines in some machine translation tasks.

We performed further analysis studies and found that our method is capable of achieving higher improvement margin compared to the baselines when the training set is small. This help the method more suitable to low-resource setups.

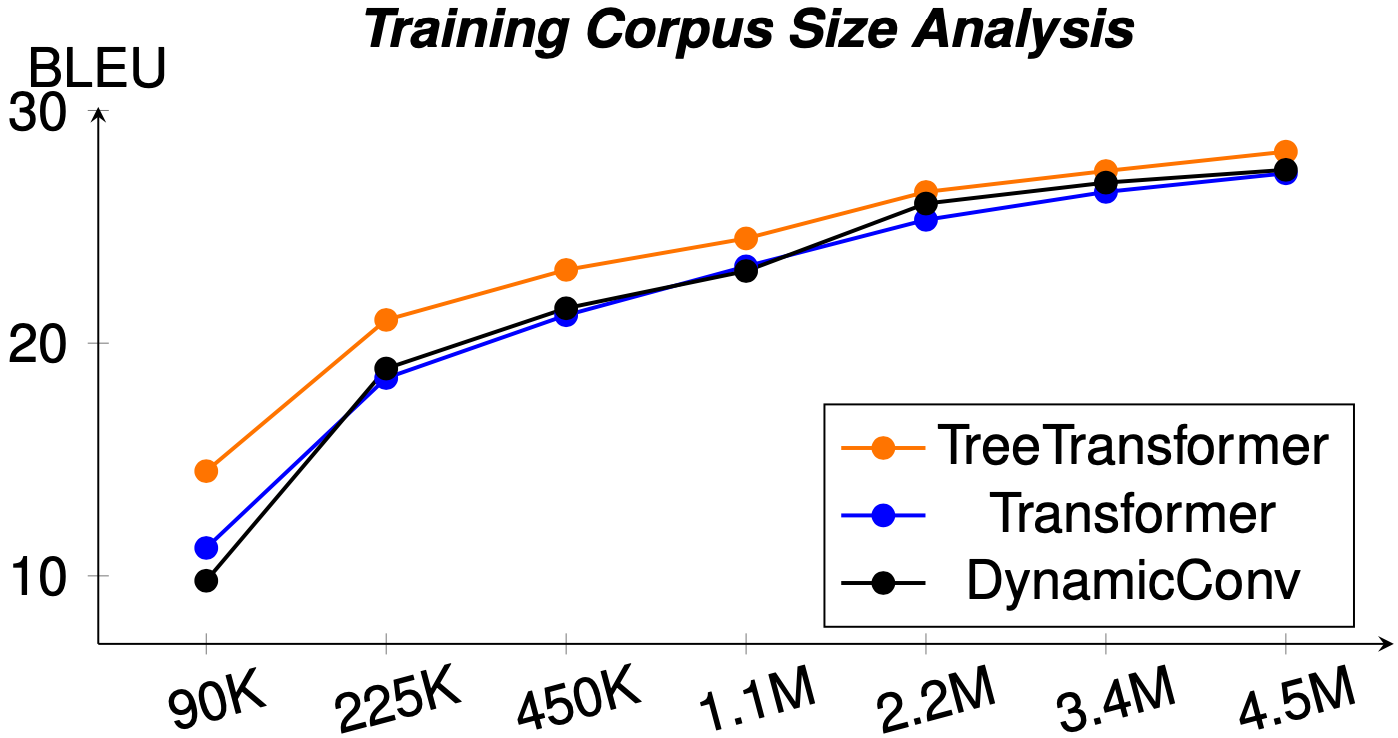
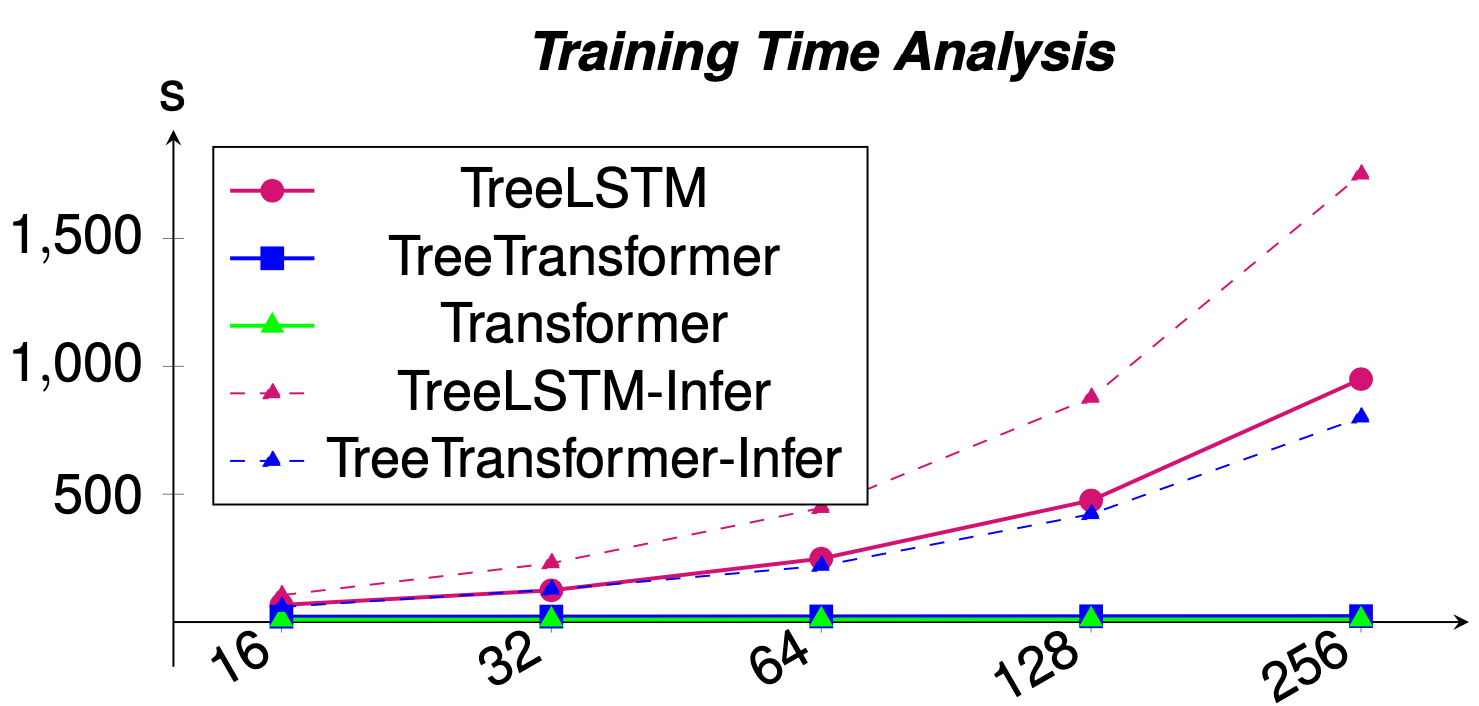
In addition, similar to the Transformer, our method process trees in O(1) parallel time complexity. This is a huge speed performance compared to the popular Tree-LSTM model, which runs at O(n) time complexity.